|
PolyFEM
|
|
PolyFEM
|
The high-level functions of PolyFEM are in polyfem::State, a class containing the application state and depending on all the PolyFEM submodules.
polyfem::assembler assembles the system matrix and right hand side (rhs). The assembler relies on finite element basis (polyfem::basis), quadrature rules (polyfem::quadrature), and for transient problems on polyfem::time_integrator.
polyfem::basis contains the implementation of finite element basis functions.
The module supports the following 2 dimensional elements:
LagrangeBasis2d.hpp)LagrangeBasis2d.hpp)SplineBasis2d.hpp)PolygonalBasis2d.hpp)The module supports the following 3 dimensional elements:
LagrangeBasis3d.hpp)LagrangeBasis3d.hpp)SplineBasis3d.hpp)PolygonalBasis3d.hpp)polyfem::mesh contains data structures and algorithms for simplicial and polygonal meshes.
The interface is generic (Mesh2D.hpp, Mesh3D.hpp). There are two specializations: a conforming implementation which supports conforming polygonal meshes (CMesh2D.hpp, CMesh3D.hpp) without hanging nodes, and a non-conforming version (CMesh2D.hpp, CMesh3D.hpp) specialized for simplicial meshes only but supporting hanging nodes, which are used to implement adaptive h-refinement.
Many input formats are supported (see the JSON documentation for the complete list), and it outputs meshes in VTU (the format used by paraview/VTK).
In PolyFEM the mesh is used to define a collection of dofs (in case of linear elements, they correspond to the nodes of the mesh, but this is not the case for other elements). The mesh is then discarded and not used by other modules.
polyfem::quadrature contains a set of quadrature rules for all elements implemented in polyfem::basis. The quadrature library is mostly independent from the rest of the codebase and it is based on the open-source library quadpy.
For transient problems, polyfem::time_integrator implements first-order (Implicit Euler ImplicitEuler.hpp) and higher-order time integrators (Implicit Newmak ImplicitNewmark.hpp, BDF BDF.hpp).
Polyfem contains right hand side, boundary conditions, exact solutions, and initial conditions for many common PDEs. We refer to the documentation in the polyfem::problem section for more details. The major physics supported by polyfem are:
From these, 1, 3–5, and 7 supports both static and transient problems, and 3–5 model contact and friction forces using the Incremental Potential Contact formulation (https://github.com/ipc-sim/ipc-toolkit).
polyfem::autogen contains python scripts to generate C++ code for:
polyfem::basispolyfem::quadraturepolyfem::assemblerThe code autogenerated by the python scripts is directly committed in the code repository, as the autogeneration is time consuming.
Smaller utilities are grouped in the polyfem::utils module, including mesh IO, hashing functions, logging, matrix utilities, parallelization, rasterization, function interpolation (RBFInterpolation.hpp), and timers (Timer.hpp).
In this section, a brief, high-level code walkthrough for a simple example problem is given.
For this example, we solve the Laplacian on a (triangular) plate-hole mesh with Dirichlet boundary conditions and a constant RHS. We choose P1 elements implicitly (as this is the default). See the JSON specificiation for more details.
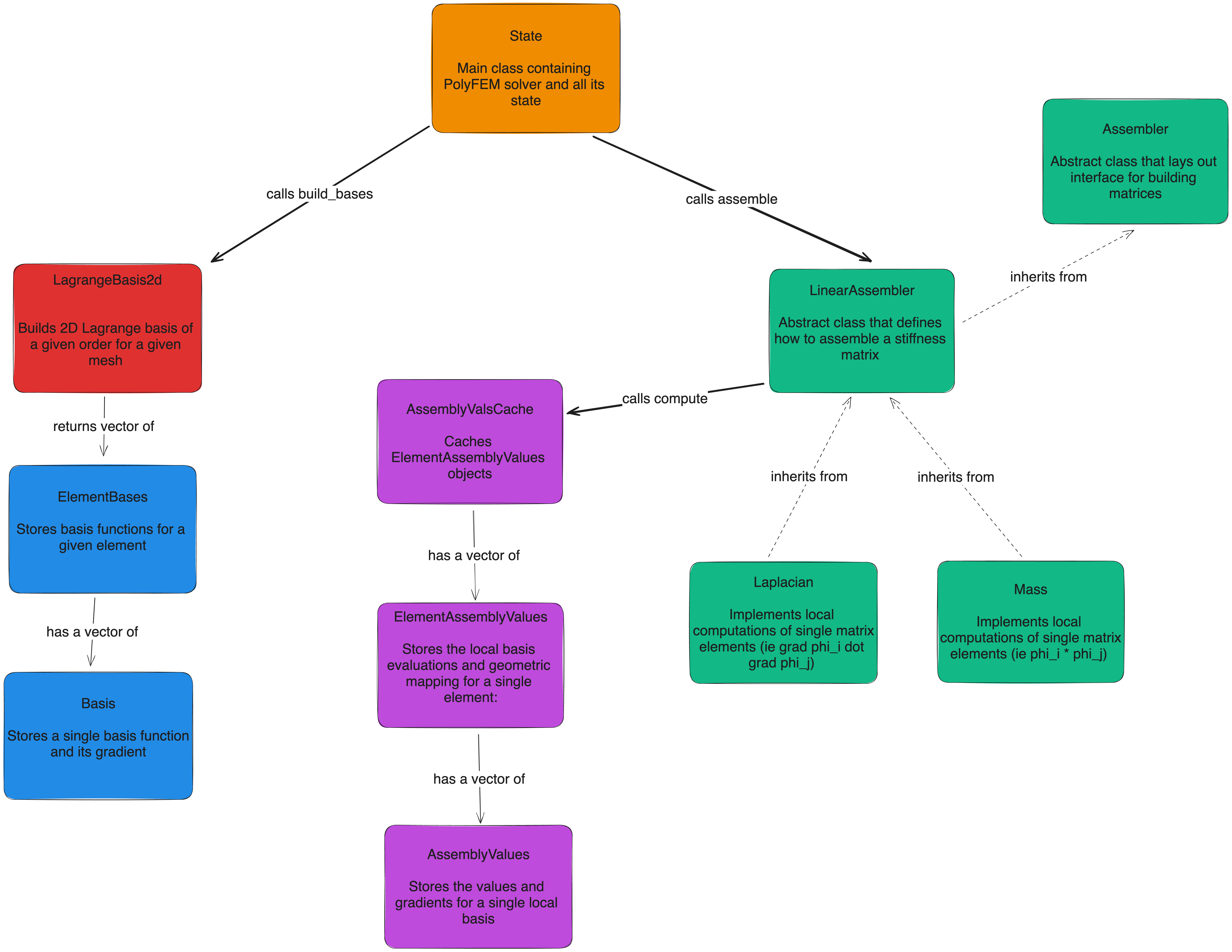
Internally, PolyFEM keeps a polyfem::State object that contains the entire state of the solve. The mesh, basis, boundary conditions, stiffness/mass matrices, RHS, and user-selected settings are all stored in polyfem::State. The polyfem::State class is also responsible for dispatch, meaning it contains member functions for the basic steps of a solve, including building a basis, assembling matrices, and actually performing the linear or nonlinear solve.
After creating a polyfem::State object and loading the input mesh, the next step in the code is to build the basis. In PolyFEM, there are two separate notions of basis: the finite element (FE) basis and the geometric basis. (They are the same in the isoparametric case.) The former is used to construct the solution whereas the latter is used to represent the geometric mapping, which is especially useful to implement curved elements.
Both the FE and geometric basis are stored as vectors of basis::ElementBases. Each basis::ElementBases object stores the basis functions for a given element as a vector of basis::Basis. Each basis::Basis stores functions representing a local basis function and its gradient.
The high-level function that constructs the FE and geometric bases is State::build_basis. In our example, it uses basis::LagrangeBasis2d to create the vector of basis::ElementBases.
In order to evaluate local basis functions and construct mass/stiffness matrices, PolyFEM makes use of a series of data storage classes. The lowest level of these classes is assembler::AssemblyValues, which stores the evaluation and gradient of a single local basis function on its element's quadrature points. A vector of basis::Local2Global objects is also stored. This is used to constrain nodes at the interface between different order elements (allowing for refinement).
The assembler::ElementAssemblyValues class stores per element information, including quadrature points in real space, the geometric mapping's determinant, and a vector of assembler::AssemblyValues objects (one for each local basis function).
Finallly, assembler::AssemblyValsCache is stores a vector of assembler::ElementAssemblyValues, boosting performance by caching the per element information. Its data can be accessed through its compute function.
These three classes are the core data storage objects used during matrix assembly. These classes use the previously constructed basis::ElementBases objects to evaluate basis functions and their gradients.
After building the basis, the next step is to assemble the RHS. This is done through the State::assemble_rhs function, which itself creates a assembler::RhsAssembler object. The assembler::RhsAssembler::assemble function is then called in order to construct the RHS vector of the weak form using assembler::AssemblyValsCache and the user-provided RHS function. In our simple example, the latter is just $10$. Note that the RHS function and boundary conditions are stored in assembler::GenericProblem.
The virtual class assembler::Assembler provides the interface used to actually construct matrices through its assemble function. For our simple example, the relevant subclass is assembler::LinearAssembler, which is itself a virtual class that defines how to assemble global matrices. However, the function that defines how to evaluate local matrix entries according to the chosen bilinear form is a pure virtual function. In our example, the stiffness matrix is built using assembler::Laplacian, which is a subclass of assembler::LinearAssembler that defines the local matrix entries (ie grad u dot grad v). The assembler::Mass class is similar except for building the mass matrix.
The relevant high-level functions for matrix assembly are State::assemble_mass_mat and State::build_stiffness_mat. Note that the stiffness matrix is built later on (in the State::solve_linear function).
After assembling the necessary matrices/vectors, the State::solve_problem function dispatches State::init_linear_solve then State::solve_problem, which solves the linear system.
A diagram showing the relationships discussed above is included below. Each block represents its own class. polyfem::State is shown in orange and basis::LagrangeBasis2d in red. The basis storage classes are blue, the value storage classes purple, and the assembly-related classes green. Relationships between classes are shown with arrows. Bold arrows represent calling a member function and dashed ones represent inheritance.
In order to boost performance, PolyFEM caches sparsity structure when assembling matrices, taking advantage of the fact that the structure of stiffness/mass matrices remains unchanged assuming the basis is unchanged. The details can be found in MatrixCache.hpp. A brief overview of polyfem::utils::SparseMatrixCache is included here for reference.
In PolyFEM, sparse matrices are stored in Compressed Sparse Column (CSC) form. Thus, the matrix is represented as three arrays: two for storing non-zero indices and one for storing values.
Consider the first time a polyfem::utils::SparseMatrixCache object is filled with values. Each time SparseMatrixCache::add_value is called, the values and their global indices are placed in a temporary buffer. It is assumed that a given polyfem::utils::SparseMatrixCache always receives each entry from a given element in the same order.
The first time the matrix is retrieved using SparseMatrixCache::get_matrix, SparseMatrixCache::prune is called, which writes the buffered values to the actual matrix. Then, the stored index information is used to create a mapping from the ordering of values received from a given element to the corresponding CSC-style index. In future iterations, instead of recomputing the matrix structure, polyfem::utils::SparseMatrixCache uses this cached index to save the given value directly to the CSC-style values array at the correct position.
All the C++ dependencies required to build the code are included and are compiled statically in a single executable. PolyFEM is compiled using automatic builds on Windows, macOS, and Linux using:
After compilation, unit and system tests (tests/main.cpp) can be run with:
Polyfem can be added to an existing cmake project with
and linked with
in your cmake script. We do not currently support other building systems. PolyFEM will download the dependencies that it needs in the build folder.